Nochmal zu Logo: Die Rekursion, d.h. der Aufruf einer Funktion durch sich selbst, sowie die Listenverarbeitung, eine Eigenschaft, die Logo als Abkömmling von LISP geerbt hat, sind mächtige Werkzeuge um elegante (und kurze) Lösungswege zu formulieren. Ich möchte das demonstrieren an den Spirolateralen.

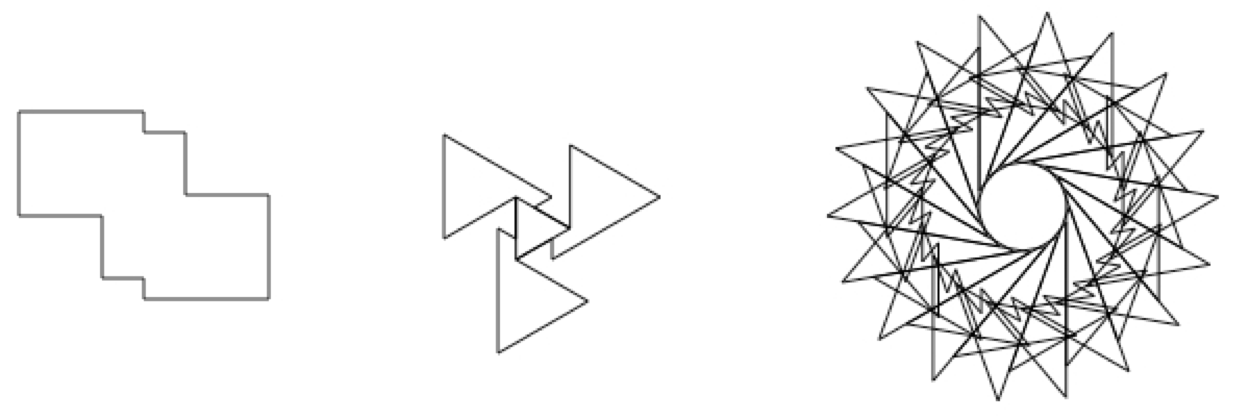
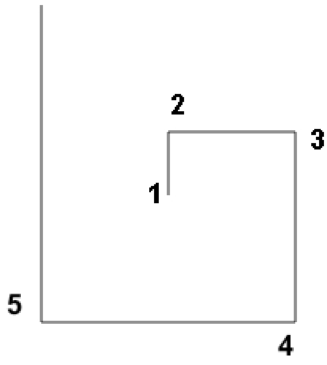Diese interessanten grafischen Gebilde sind in ihrer Grundform sehr simpel zu konstruieren: Begonnen wird mit einer Linie bestimmter Länge gefolgt von einer Rechtsdrehung um 90 Grad. Daran angesetzt wird die nächste Linie mit doppelter Länge, es folgt erneut eine 90 Grad-Drehung, dann eine Linie mit dreifacher Länge usw. Dies wird bis zu einer maximal vorgegebenen Anzahl von Iterationen fortgesetzt (im Beispiel rechts also fünf mal). Diese Schleife kann nun mehrfach wiederholt werden. Der ganze Vorgang wird abgebrochen, wenn die Schildkröte ihren Ursprungsort erreicht hat.

Das Ergebnis der mehrfachen Abfolge solcher Schleifen ist hier von n=1 bis n=6 abgebildet und verdeutlicht das einfache Grundprinzip.

Wir definieren dazu eine Prozedur spirolaterale. Aufgerufen wird dort die Prozedur spiro (in der die Linien gezeichnet werden) mit Übergabe einer Variablen max, die angibt, wie oft Linien und Drehungen vollzogen werden sollen. Danach wird geprüft, ob die Schildkröte ihren Ausgangspunkt erreicht hat. Falls ja, wird die Prozedur beendet, falls nein, wird spirolaterale erneut ausgeführt (endständige Rekursion). Der Aufruf spirolaterale 15 führt dann zum Ergebnis in der rechten Abbildung.

Bevor ich die Prozeduren zeige, möchte ich sie erst gleich erweitern um Listen, die berühmte LISP-Erbschaft. Sie helfen uns, Antworten zu finden auf Fragen wie: Was passiert, wenn die Linien nicht konstant wachsen, sondern ihre Länge für jeden Schritt frei festgelegt werden kann? Was passiert, wenn ich andere als rechte Winkel nehme? Und was passiert, wenn nicht nur Rechtsdrehungen, sondern auch Linksdrehungen erlaubt sind? Dazu führen wir eine Variable winkel ein. Und nun kommen die Listen ins Spiel.

In einer ersten Liste listefaktor können wir gemäß der Linienabfolge nach jeder Drehung den jeweiligen Verlängerungsfaktor der Linie angeben. In einer zweiten Liste listedrehung legen wir dann fest, ob die dann anstehende Drehung nach rechts oder nach links erfolgen soll. Daa kann unterschiedlich umgesetzt werden, z.B. eine Liste [R R L R L], wobei R für Rechtsdrehung, L für Linksdrehung stehen soll. Ich bevorzuge eine Listenform [1 1 -1 1 -1], bei der die 1 für Rechtsdrehung, -1 für Linksdrehung steht. Dies macht die Verrechnung schneller. So, die entsprechenden Prozeduren sehen dann so aus:

Prozedur spirolaterale winkel listefaktor listedrehung>spiro :winkel :listefaktor :listefaktor
if (and (abs xpos) < 1 (abs ypos) < 1) [stop]
[spirolaterale :winkel :listelfaktor :listedrehung]

Prozedur spiro winkel listefaktor listedrehung
if empty? :listefaktor [stop]
[forward 10*first :listefaktor right :w*first :listedrehung
spiro :winkel butfirst :listefaktor butfirst listedrehung

Spirolaterale 90 [1 2 3 4 5 6 ] [1 1 1 1 1 1] reproduziert die Grundfigur mit n=6 (s.0.). Mit spirolaterale 90 [1 2 3 4 5 6 ] [-1 1 -1 1 1 1], also mit zwei Linksdrehungen kommt die Figur unten links heraus und bei einer Winkeländerung auf 120 Grad , d.h. spirolaterale 120 [1 2 3 4 5 6 ] [-1 1 -1 1 1 1] kommt die Figur unten Mitte heraus. In dem Artikel Investigating Spirolaterals through LOGO von Fisher & Campbell finden sich sowohl nachvollziehbare mathematische Hintergründe zu den Spirolateralen und viele Beispiele, die nun mit der hier erreichten Variabilität alle leicht nachvollzogen werden können. Auch Krawczyk hat in The Art of Spirolaterals entsprechende Varianten vorgestellt, z.B. mit spirolaterale 220 [7 5 3 1 3 5 7 ] [1 1 1 -1 1 1 1] die Figur unten rechts.